Box-Whisker Plots

require(tlf)
#> Loading required package: tlf

1. Introduction

The following vignette aims at documenting and illustrating workflows for producing box-and-whisker plots using the tlf-Library.

This vignette focuses boxplot examples. Detailed documentation on typical tlf workflow, use of AgregationSummary, DataMapping, PlotConfiguration and Theme can be found in vignette("tlf-workflow").

2. Definition of the boxplot functions and classes

2.1. The plotBoxWhisker function

The function for plotting box-whiskers is: plotBoxWhisker. Basic documentation of the function can be found using: ?plotBoxWhisker. The typical usage of this function is: plotBoxWhisker(data, metaData = NULL, dataMapping = NULL, plotConfiguration = NULL). The output of the function is a ggplot object.

2.2. The BoxWhiskerDataMapping class

The dataMapping from plotBoxWhisker requires a BoxWhiskerDataMapping class. This class can simply be initialized by BoxWhiskerDataMapping$new(), needing y variable name input only. For boxplots with multiple boxes, x variable name and/or fill groupMapping can be used. The x variable is expected to be factor levels. Beside these common input, it is possible to overwrite the aggregation functions that plot the edges of the box, the whiskers and the outlying data.

• For the box edges lower, middle, and upper correspond to the first quartile, median, and the third quartile (25th, 50th, and 75th percentiles), respectively.
• For the whiskers, ymin and ymax use the 5th and 95th percentiles.
• For outliers, points lower than the 25th percentile - 1.5 x IQR and points higher than 75th percentile + 1.5 x IQR (where IQR is the inter-quartile range) are flagged and plotted.

In order to help with the boxplot aggregation functions, a bank of predefined function names is already available in the tlfStatFunctions (as an enum). Consequently, a tree with the available predefined function names will appear when writing tlfStatFunctions$: ‘mean’, ‘sd’, ‘min’, ‘max’, ‘mean-sd’, ‘mean+sd’, ‘mean-1.96sd’, ‘mean+1.96sd’, ‘Percentile0%’, ‘Percentile1%’, ‘Percentile2.5%’, ‘Percentile5%’, ‘Percentile10%’, ‘Percentile15%’, ‘Percentile20%’, ‘Percentile25%’, ‘Percentile50%’, ‘Percentile75%’, ‘Percentile80%’, ‘Percentile85%’, ‘Percentile90%’, ‘Percentile95%’, ‘Percentile97.5%’, ‘Percentile99%’, ‘Percentile100%’, ‘median-IQR’, ‘median+IQR’, ‘median-1.5IQR’, ‘median+1.5IQR’, ‘Percentile25%-1.5IQR’, ‘Percentile75%+1.5IQR’,

3. Examples

3.1. Data

To illustrate the workflow to produce boxplots, let’s use the pkRatioDataExample.RData example data from the extdata folder.

It includes the dataset pkRatioData:

# Load example
pkRatioData <- read.csv(
  system.file("extdata", "test-data.csv", package = "tlf"),
  stringsAsFactors = FALSE
)

# pkRatioData
knitr::kable(utils::head(pkRatioData), digits = 2)

ID	Age	Obs	Pred	Ratio	AgeBin	Sex	Country	SD
1	48	4.00	2.90	0.72	Adults	Male	Canada	0.69
2	36	4.40	5.75	1.31	Adults	Male	Canada	0.19
3	52	2.80	2.70	0.96	Adults	Male	Canada	0.98
4	47	3.75	3.05	0.81	Adults	Male	Canada	0.59
5	0	1.95	5.25	2.69	Peds	Male	Canada	0.44
6	48	2.45	5.30	2.16	Adults	Male	Canada	0.07

We will also need to prepare a corresponding metaData pkRatioMetaData:

# Load example
pkRatioMetaData <- list(
  Age = list(
    dimension = "Age",
    unit = "yrs"
  ),
  Obs = list(
    dimension = "Clearance",
    unit = "dL/h/kg"
  ),
  Pred = list(
    dimension = "Clearance",
    unit = "dL/h/kg"
  ),
  Ratio = list(
    dimension = "Ratio",
    unit = ""
  )
)

knitr::kable(data.frame(
  Variable = c("Age", "Obs", "Pred", "Ratio"),
  Dimension = c("Age", "Clearance", "Clearance", "Ratio"),
  Unit = c("yrs", "dL/h/kg", "dL/h/kg", "")
))

Variable	Dimension	Unit
Age	Age	yrs
Obs	Clearance	dL/h/kg
Pred	Clearance	dL/h/kg
Ratio	Ratio

3.2. Minimal example

In the minimal example, only the basic y variable name is indicated. Here, "Age" was chosen for the boxplot.

minMap <- BoxWhiskerDataMapping$new(y = "Age")

minBoxplot <- plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = minMap
)
minBoxplot

3.3. Difference x vs fill input

In this plot, x and/or fill can be provided. If only x is provided, the plot will use the x variable for aggregation and the boxplots will be displayed according to x. If providing fill, the plot will use the fill groupMapping for aggregation and the boxplots will be displayed around the same x but comparing the color filling. Consequently, the fill variable is useful when performing a double comparison.

In the example below, "Country" and "Sex" can both be used for comparison of "Age".

xPopMap <- BoxWhiskerDataMapping$new(
  x = "Country",
  y = "Age"
)

xSexMap <- BoxWhiskerDataMapping$new(
  x = "Sex",
  y = "Age"
)

fillPopMap <- BoxWhiskerDataMapping$new(
  y = "Age",
  fill = "Country"
)

fillSexMap <- BoxWhiskerDataMapping$new(
  y = "Age",
  fill = "Sex"
)
xPopFillSexMap <- BoxWhiskerDataMapping$new(
  x = "Country",
  y = "Age",
  fill = "Sex"
)

xSexFillPopMap <- BoxWhiskerDataMapping$new(
  x = "Sex",
  y = "Age",
  fill = "Country"
)

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xPopMap
)

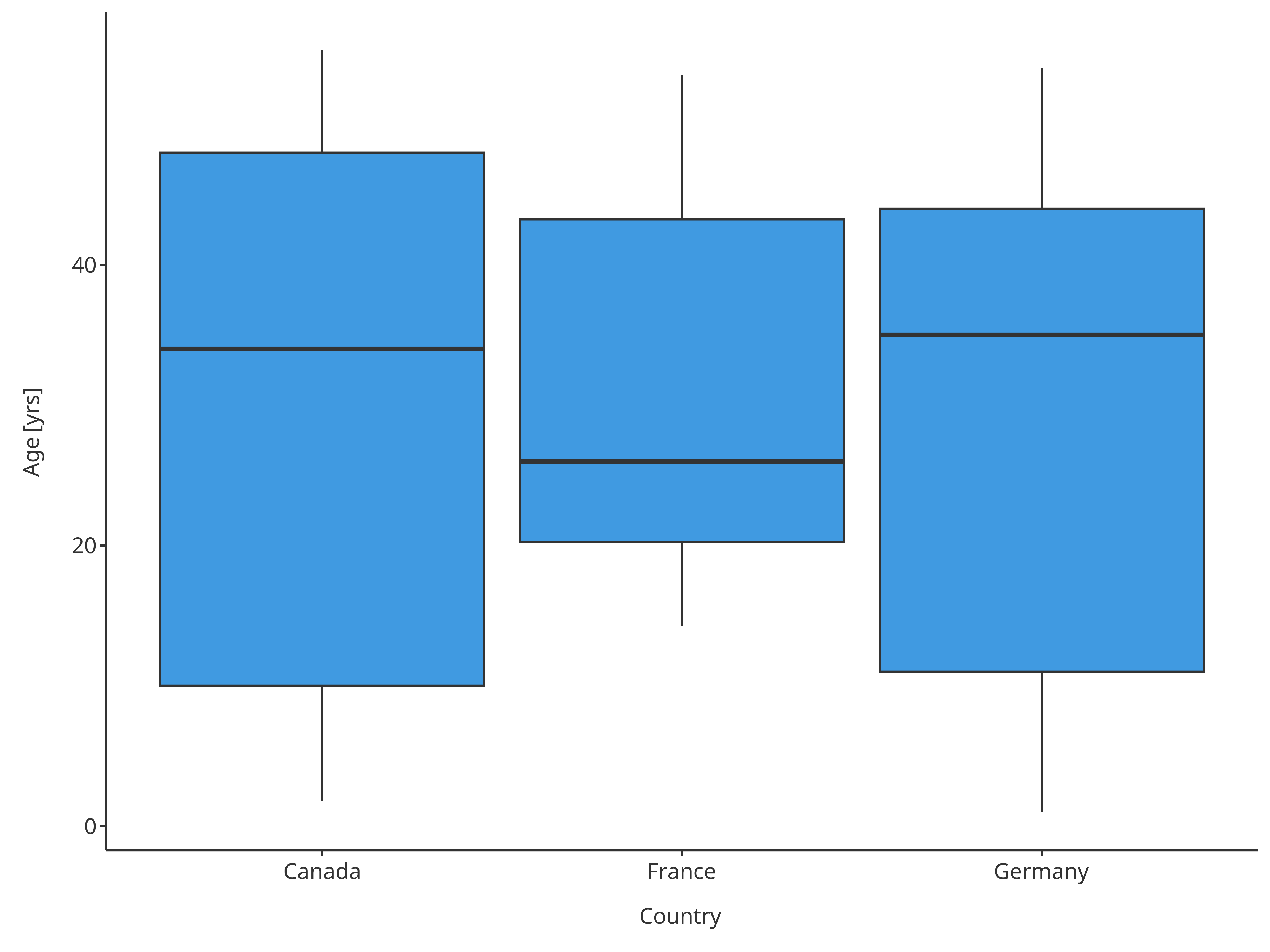
Boxplot mapping Country as x

Note that the sample from a given country sometimes did not have any individual from one of the sexes.

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xSexMap
)

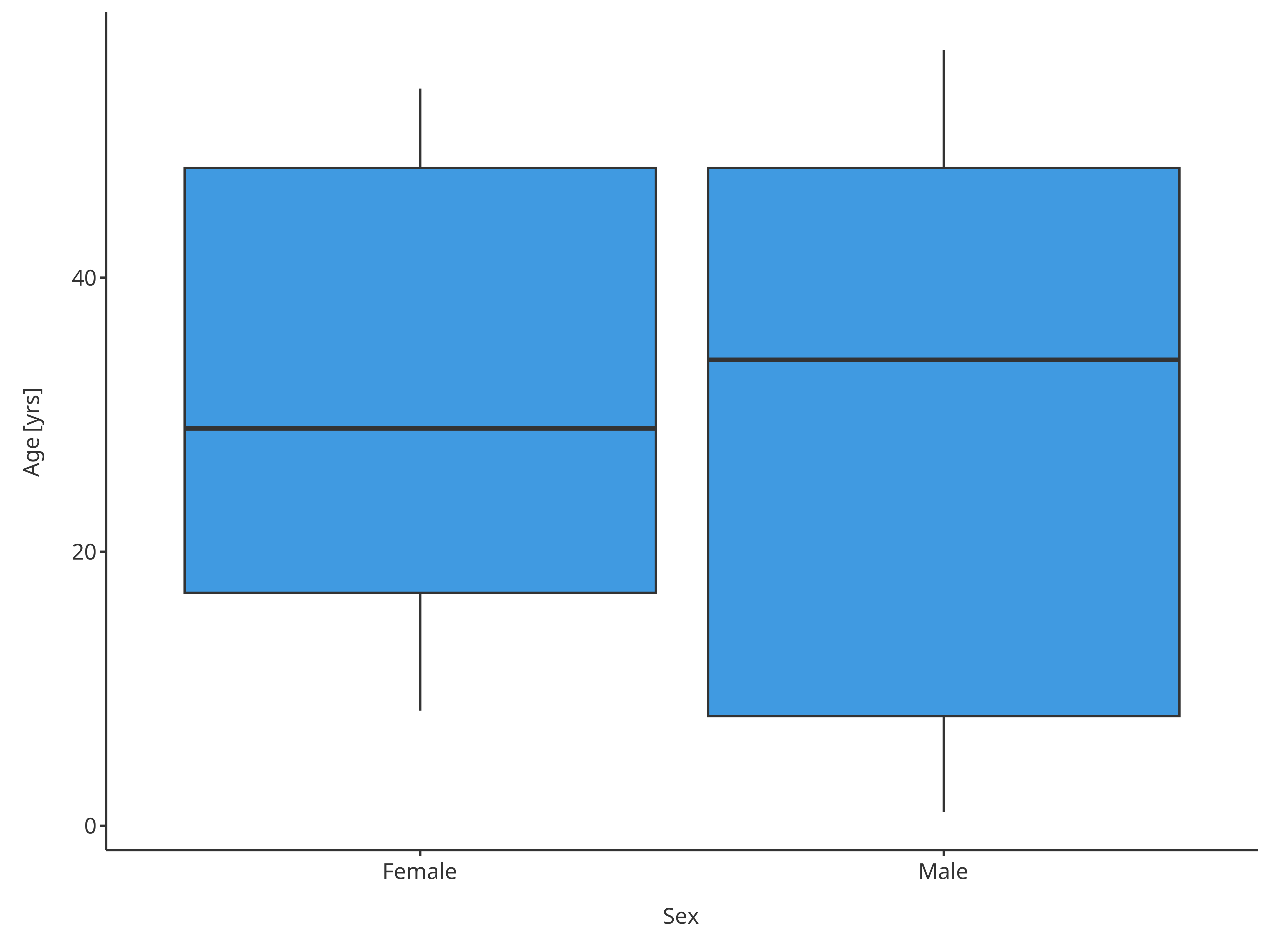
Boxplot mapping Sex as x

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = fillPopMap
)

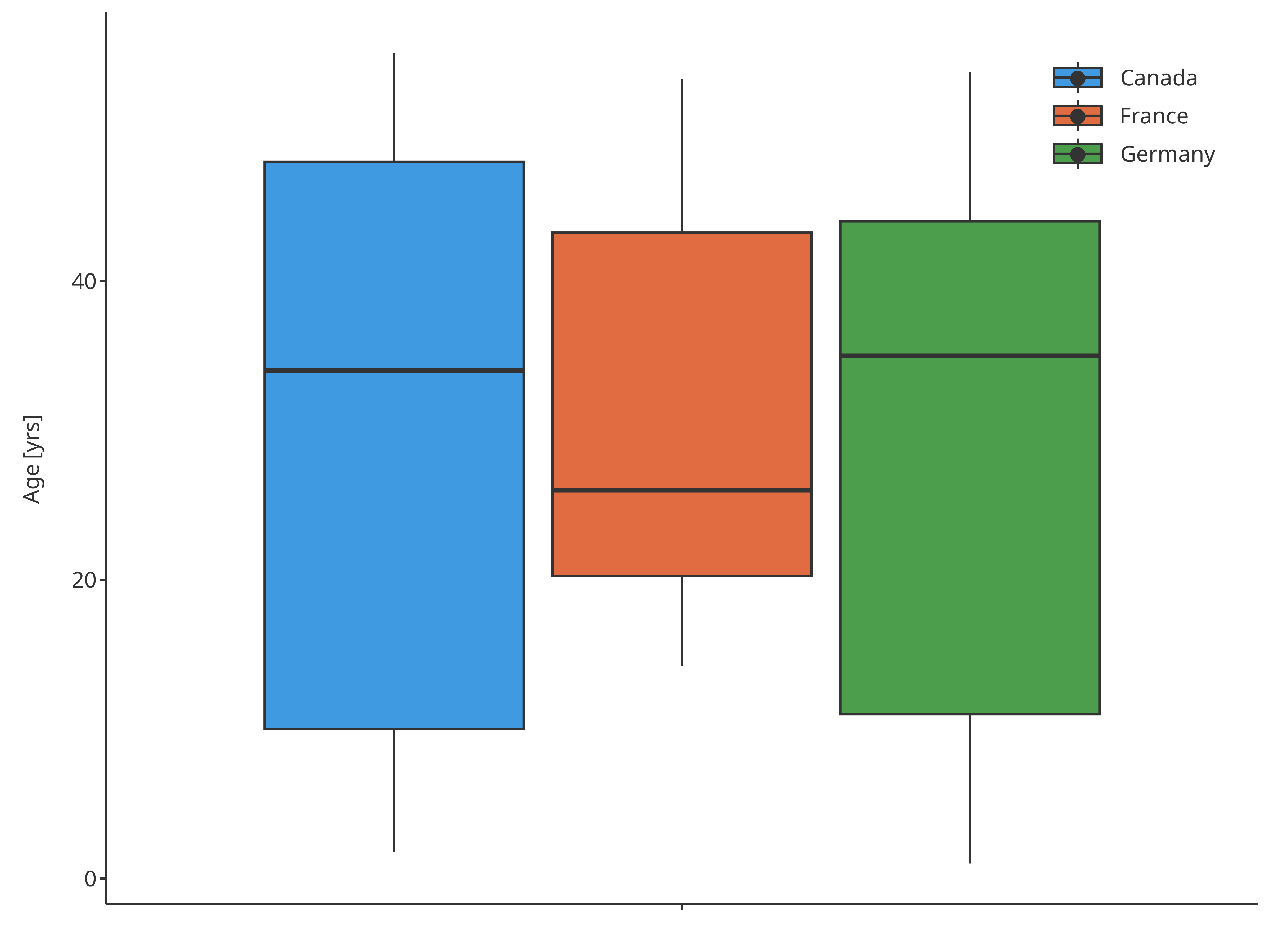
Boxplot mapping Country as fill

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = fillSexMap
)

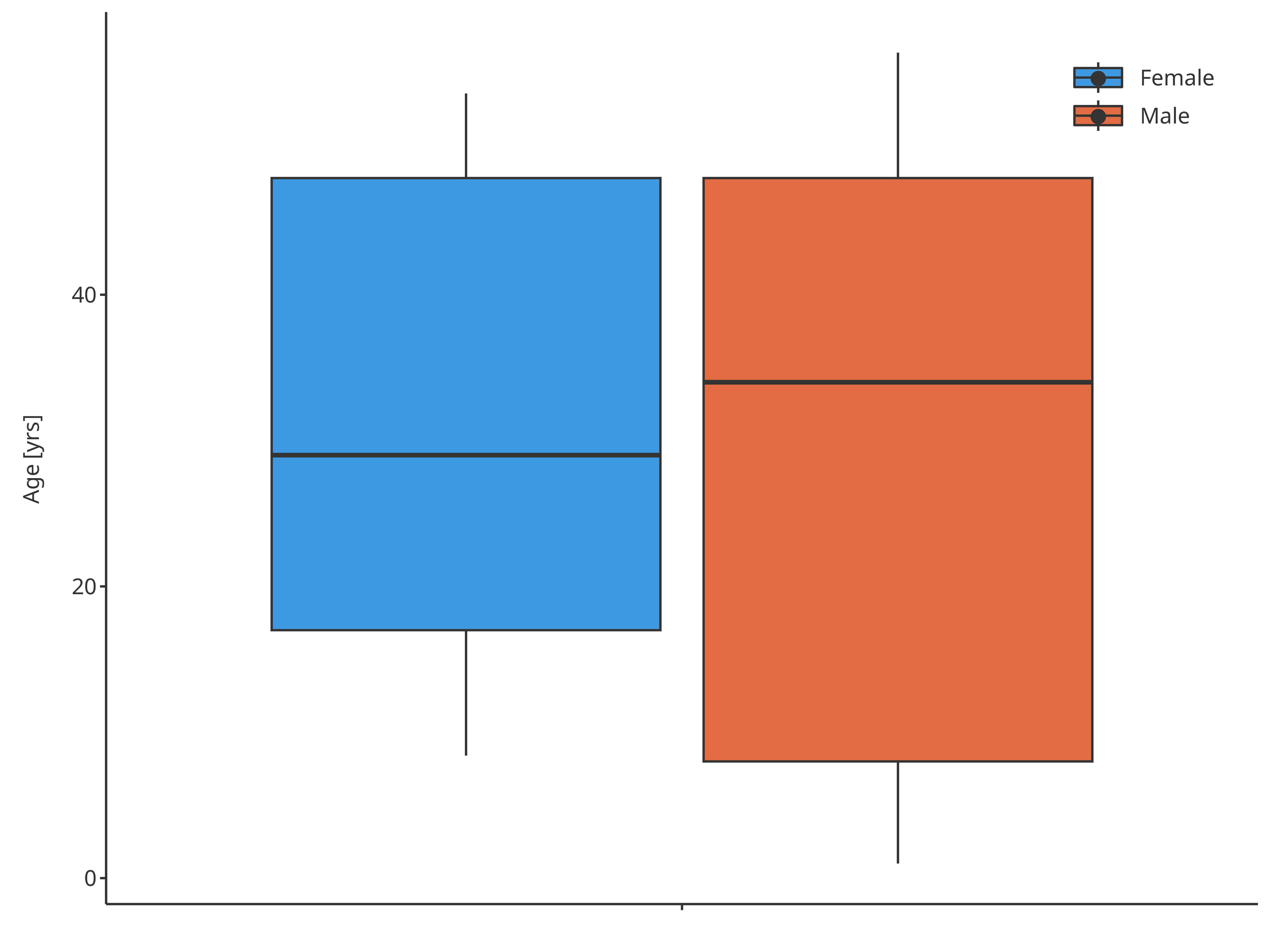
Boxplot mapping Sex as fill

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xPopFillSexMap
)

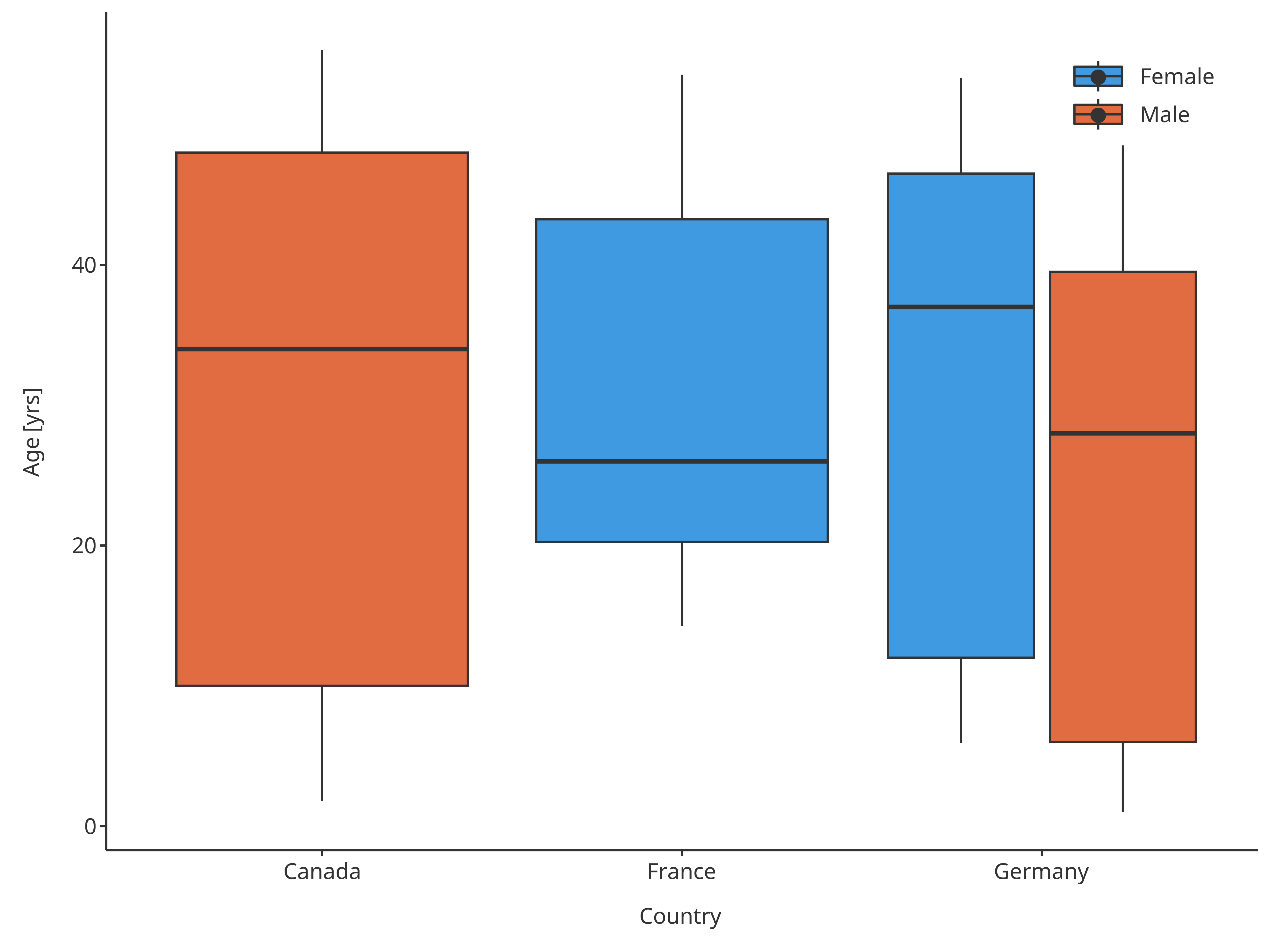
Boxplot mapping Country as x and Sex as fill

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xSexFillPopMap
)

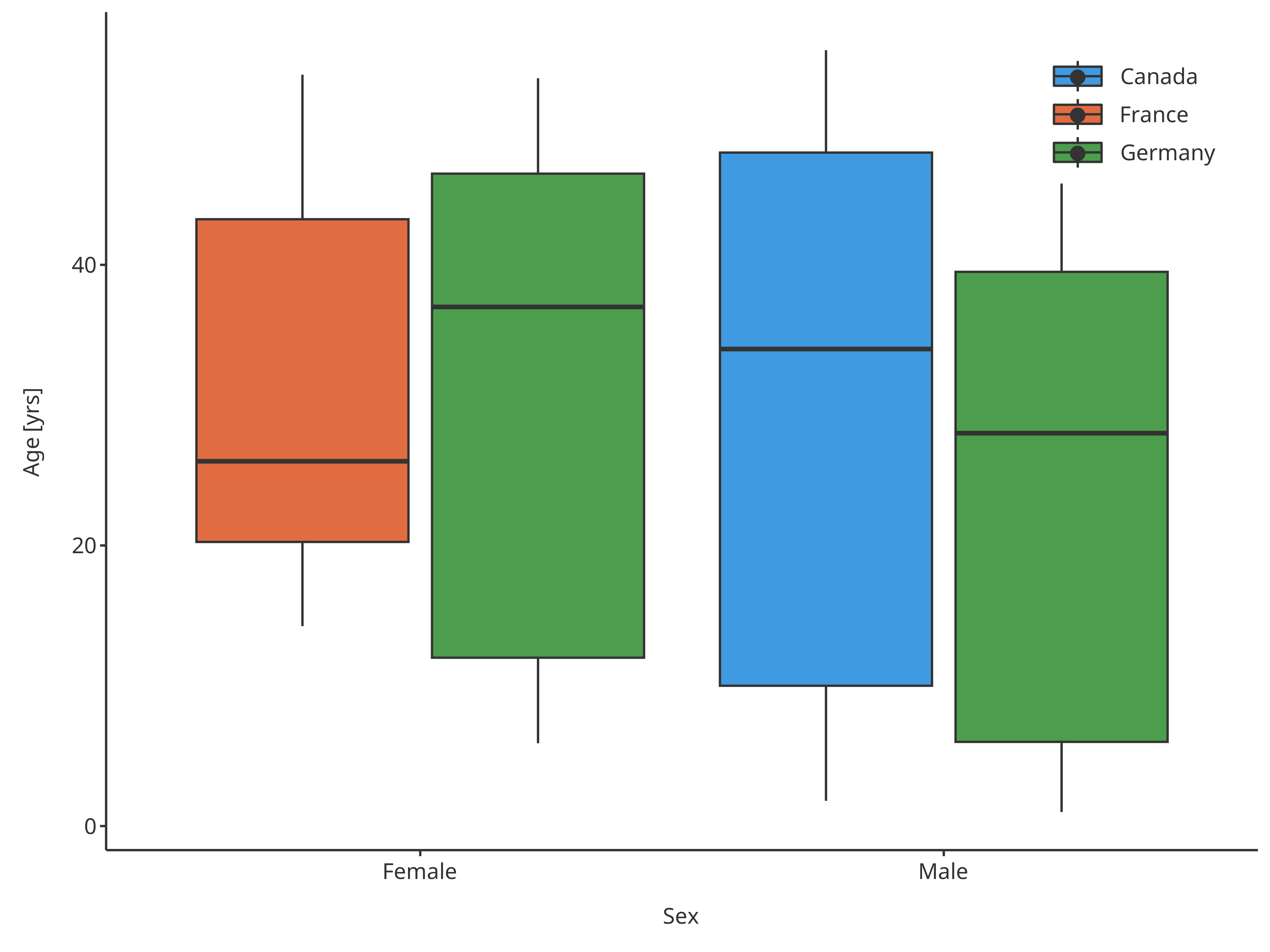
Boxplot mapping Sex as x and Country as fill

3.4. Boxplot functions

In some cases, displaying 5th and 95th percentiles is not necessary. For instance, when a normal distribution is assumed, mean +/- 1.96 standard deviation would be preferred. In these cases, it is easy to overwrite the default functions by specifying either using a home made function or directly using predefined functions as suggested in section 2.2.

In the following examples, the boxplot will use the mean for the middle line and mean +/- 1.96 standard deviation for the whiskers:

normMap <- BoxWhiskerDataMapping$new(
  x = "Country",
  y = "Age",
  fill = "Sex",
  ymin = tlfStatFunctions$`mean-1.96sd`,
  middle = tlfStatFunctions$mean,
  ymax = tlfStatFunctions$`mean+1.96sd`
)

normBoxplot <- plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = normMap
)
normBoxplot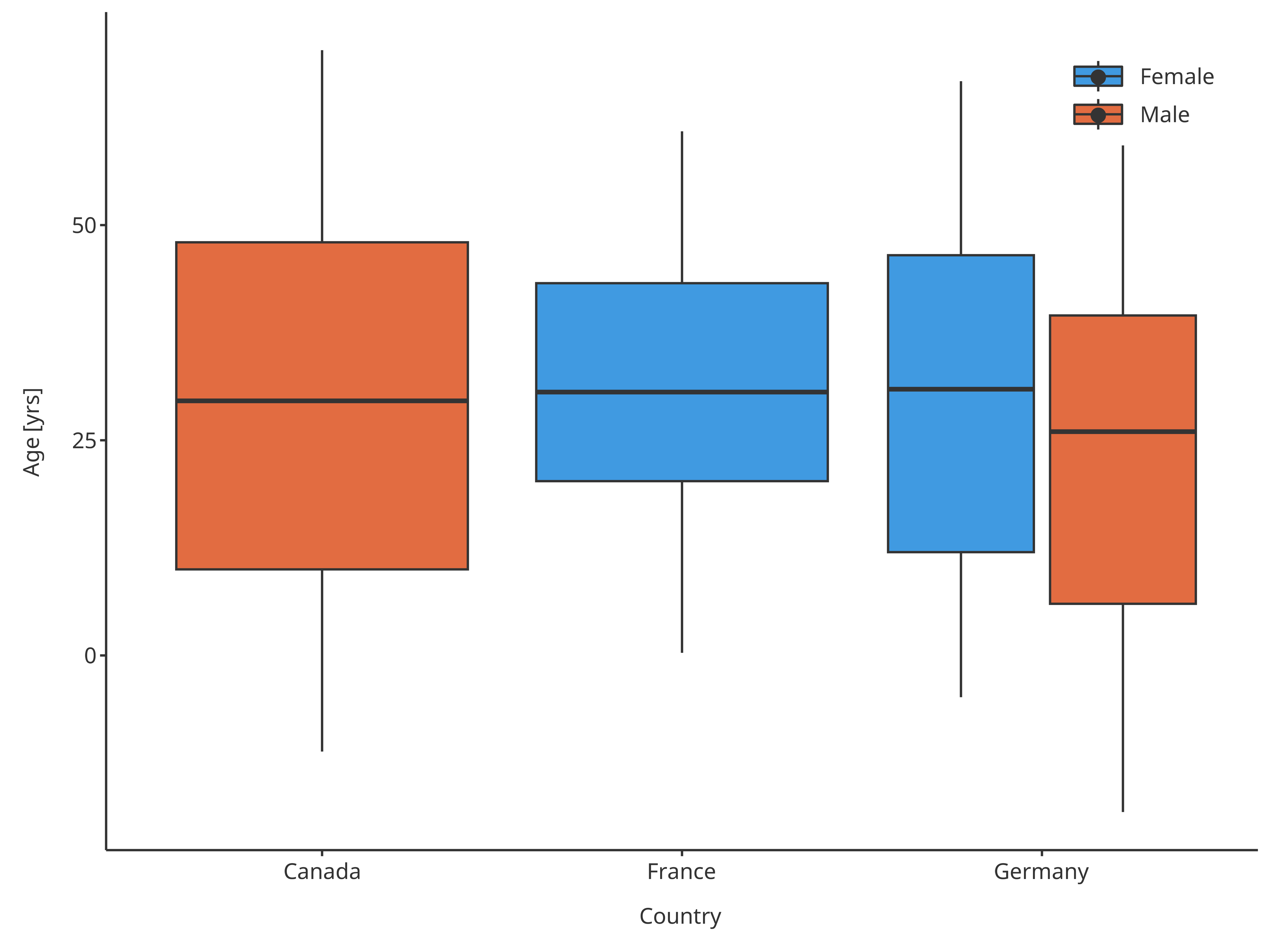

Boxplot mapping Country as x, Sex as fill and assuming normal distribution

In this example, the boxplot use also mean +/- standard deviation for the box edges

normMap2 <- BoxWhiskerDataMapping$new(
  x = "Country",
  y = "Age",
  fill = "Sex",
  ymin = tlfStatFunctions$`mean-1.96sd`,
  lower = tlfStatFunctions$`mean-sd`,
  middle = tlfStatFunctions$mean,
  upper = tlfStatFunctions$`mean+sd`,
  ymax = tlfStatFunctions$`mean+1.96sd`
)

normBoxplot2 <- plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = normMap2
)
normBoxplot2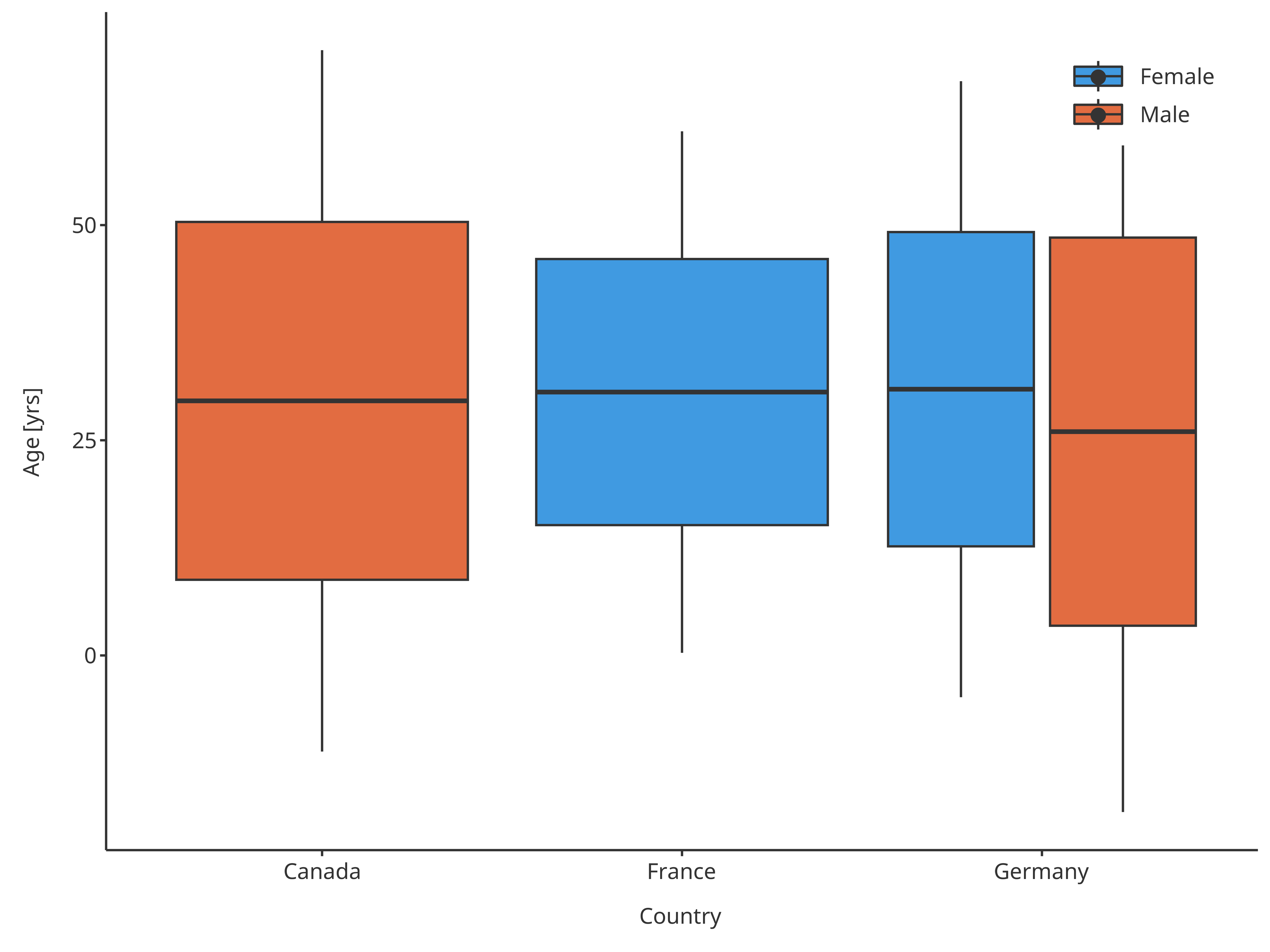

Boxplot mapping Country as x, Sex as fill and assuming normal distribution

Important: If you override the defaults this way, please make sure to specify this in the plot annotations as you are basically redefining a boxplot and the reader might not be aware of this and will misinterpret the plot.

3.5. Outlier functions

Default outliers are flagged when outside the range from 25th percentiles - 1.5 x IQR to 75th percentiles + 1.5 x IQR, as suggested by McGill and implemented by the current boxplot functions from ggplot (geom_boxplot). However, these default can also be overridden.

In the following example, outliers will be flagged when values are out of the 10th-90th percentiles, while whiskers will go until these same percentiles:

outlierMap <- BoxWhiskerDataMapping$new(
  x = "Country",
  y = "Age",
  fill = "Sex",
  ymin = tlfStatFunctions$`Percentile10%`,
  ymax = tlfStatFunctions$`Percentile90%`,
  minOutlierLimit = tlfStatFunctions$`Percentile10%`,
  maxOutlierLimit = tlfStatFunctions$`Percentile90%`
)

outlierBoxplot <- plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = outlierMap
)
outlierBoxplot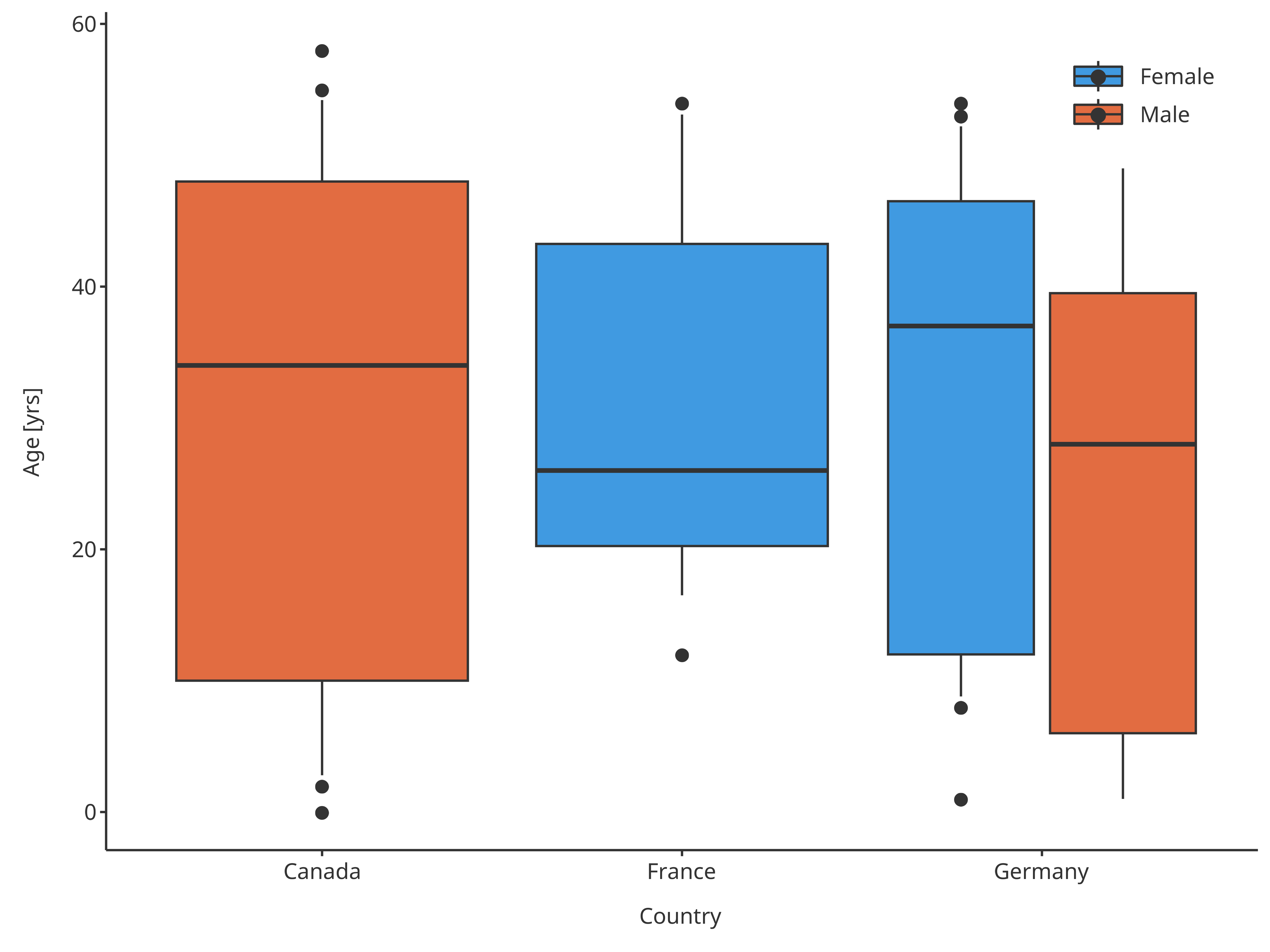

Boxplot mapping Country as x, Sex as fill and assuming normal distribution

3.4. plotConfiguration of boxplots: BoxWhiskerPlotConfiguration

To define the properties of the boxes and points of the box whisker plots, a BoxWhiskerPlotConfiguration object can be defined to overwrite the default properties. The ribbons and points fields will define how the boxes and outliers will be handled.

Using the previous example where country was defined in x and gender as color.

# Define a PlotConfiguration object using smart mapping
boxplotConfiguration <- BoxWhiskerPlotConfiguration$new(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xPopFillSexMap
)

# Change the properties of the box colors
boxplotConfiguration$ribbons$fill <- c("pink", "dodgerblue")
boxplotConfiguration$ribbons$color <- "orange"

# Change the properties of the points (outliers)
boxplotConfiguration$points$size <- 2
boxplotConfiguration$points$shape <- Shapes$diamond

plotBoxWhisker(
  data = pkRatioData,
  metaData = pkRatioMetaData,
  dataMapping = xPopFillSexMap,
  plotConfiguration = boxplotConfiguration
)

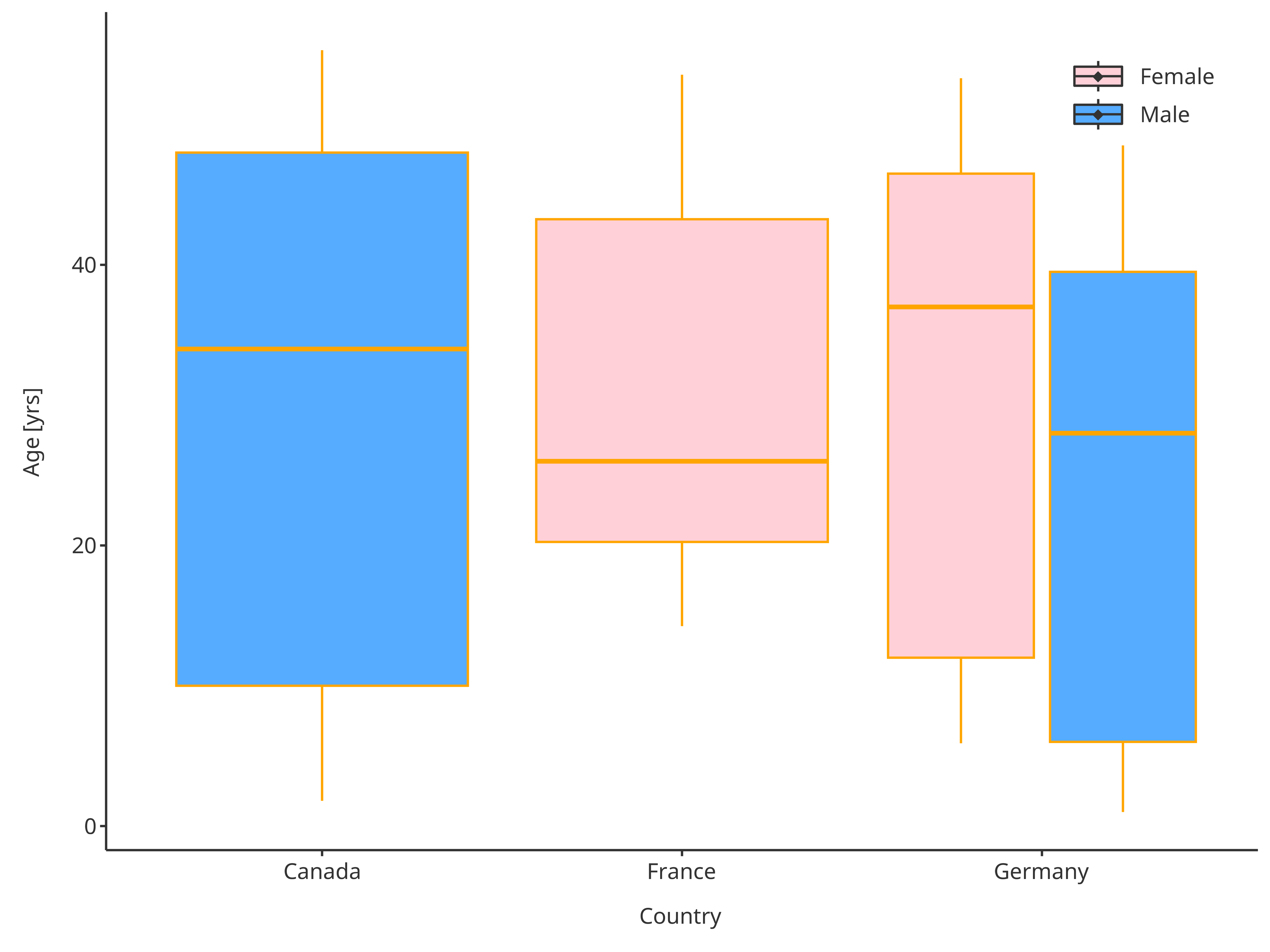
Boxplot with updated plot configuration

4. Further utility of BoxWhiskerDataMapping

Since the boxplot data mapping performs an aggregation of the data, it possible to get directly the resulting aggregated statistic as a table using getBoxWhiskerLimits(). Similarly, it can be used to flag any values out of a certain range using getOutliers().

For instance, using the example from section 3.5, one can get the following results

boxplotSummary <- outlierMap$getBoxWhiskerLimits(pkRatioData)

knitr::kable(boxplotSummary, digits = 2)

Country	Sex	ymin	lower	middle	upper	ymax	legendLabels
France	Female	16.5	20.25	26	43.25	53.1
Germany	Female	8.8	12.00	37	46.50	52.2
Canada	Male	2.8	10.00	34	48.00	54.2
Germany	Male	1.0	6.00	28	39.50	49.0

outliers <- outlierMap$getOutliers(pkRatioData)
outliers <- outliers[, c("Age", "minOutlierLimit", "maxOutlierLimit", "minOutliers", "maxOutliers")]

knitr::kable(utils::head(outliers), digits = 2)

Age	minOutlierLimit	maxOutlierLimit	minOutliers	maxOutliers
48	2.8	54.2	NA	NA
36	2.8	54.2	NA	NA
52	2.8	54.2	NA	NA
47	2.8	54.2	NA	NA
0	2.8	54.2	0	NA
48	2.8	54.2	NA	NA